Arquímedes PI
Introducción
En matemáticas π es una constante cuyo valor es la razón entre el perímetro de un círculo con respecto a su diámetro, es decir, cuantas veces cabe el diámetro en el perímetro del círculo.

Arquímedes de Siracusa(ca. 287 a ca. 212 a. C.) fue un matemático griego, físico, ingeniero, inventor y astrónomo. Él fue probablemente el primero en encontrar un método para aproximar el valor de π de manera iterativa.
Dada una circunferencia, el método de Arquímedes consiste en dibujar un polígono inscrito y otro circunscrito y calculaba el perímetro de ambos polígonos, siendo estos perímetros el límite superior(polígono circunscrito) y límite inferior(polígono inscrito).
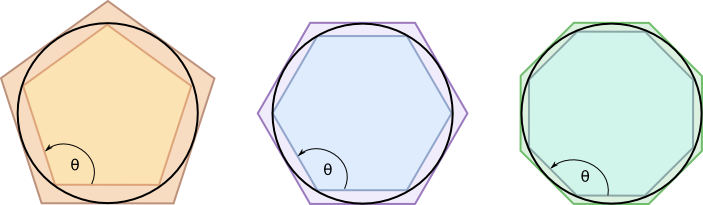
Con base en lo anterior Arquímedes pudo determinar el intervalo numérico en el que se encuentra el valor exacto de π.
$$3+\frac{10}{71}<\pi<3+\frac{1}{7}$$
Sabemos que el perímetro de una circunferencia es igual a 2 * π * radio o π * diámetro y que el perímetro de un polígono regular de n lados es n * longitudDeLado. Las siguientes fórmulas obtienen el valor aproximado de π para para los límites inferior y superior para polígonos inscritos y circunscritos respectivamente.
$$p = 2rsin(\frac{\theta}{2})n \approx \pi$$
$$p = 2rtan(\frac{\theta}{2})n \approx \pi$$
Donde n es el número de lados del polígono, r el radio de la circunferencia y θ es el ángulo interno formado por los lados del polígono. Para un caso general podemos asumir que el diámetro del círculo es igual a la unidad, por tanto $r=\frac{1}{2}$, reduciendo las anteriores fórmulas a:
$$p = sin(\frac{\theta}{2})n \approx \pi$$
$$p = tan(\frac{\theta}{2})n \approx \pi$$
Según estas fórmulas solo necesitamos conocer el valor de n, el cual lo sabemos de antemano y el valor de θ, que calculamos con
$$\frac{2\pi}{n}~~~~~~siendo~\pi=3.14159$$
En la ecuación se remarca que en esta fórmula debe emplearse el valor de π con la precisión que empleamos comúnmente para el calculo de θ.
Por cierto, si se preguntan de donde resultan las formulas una imagen puede ayudar:
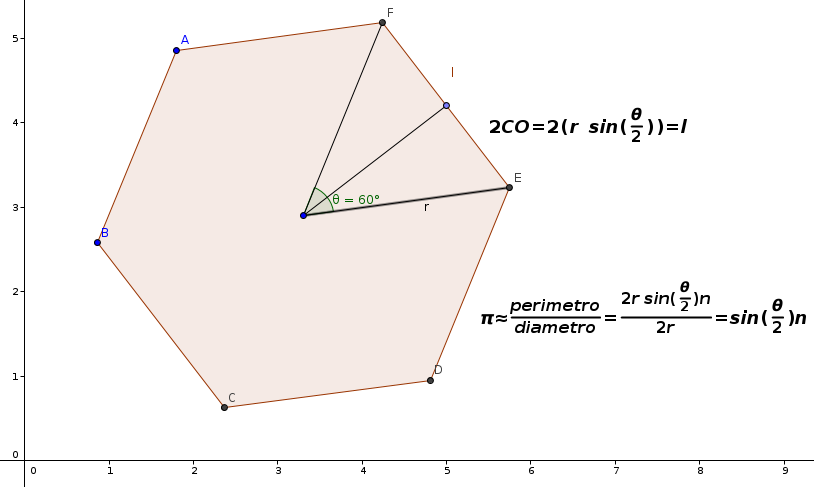
Cuanto mayor sea el número de lados del polígono mayor sera la precisión del valor de
π
. Así, por ejemplo, para n = 3, n = 8 y n = 17280 usando un polígono inscrito tenemos que el valor aproximado de
π
es 2.598076211353316, 3.0614674589207183 y 3.1415926362832276 respectivamente.
Aplicaciones
Hoy por la mañana me levante y por suerte tenía un poco de tiempo libre así que prendí mi ordenador y decidí entrar la arena de Topcoder y practicar un poco(para no quedar en los últimos lugares como siempre) y entonces me encontré con el problema Archimedes empleado en el SRM 151. Sinceramente no tuve idea de como resolver el problema, así que investigue un poco y pude resolver el problema. En este post he expuesto lo que encontré, espero que les sirva. Les dejo la solución del problema en C++ por si acaso.
#include <cmath>
#include <iostream>
using namespace std;
class Archimedes
{
public:
double approximatePi(int numSides) {
double pi = acos(-1);
double angle = 2 * pi / numSides;
return numSides * sin(angle / 2);
}
};
int main()
{
Archimedes archimedes;
cout << archimedes.approximatePi(4) << endl;
return 0;
}