De poligonos y estrellas
Hace algun tiempo tuve la necesidad de desarrollar una aplicación en Java que dibujara polígonos regulares y estrellas de n lados y n picos respectivamente para una materia en la escuela. En un principio me fue difícil solucionar este problema pero al final encontré la manera. A continuación comento en que consiste la solución.
Es común que la mayoría de nosotros estemos familiarizados con el sistema de coordenadas rectangulares donde cada punto en el espacio se representa por dos valores de la forma (x, y) donde x, y ∈ ℝ, x corresponde al desplazamiento sobre la recta horizontal y y corresponde al desplazamiento vertical. Véase figura .
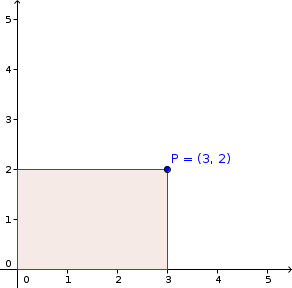
Con este sistema de coordenadas es posible representar cualquier objeto geométrico, incluyendo nuestros polígonos, sin embargo existen otros sistemas de coordenadas que nos facilitan las cosas para esta tarea en especial, me refiero a las coordenadas polares.:
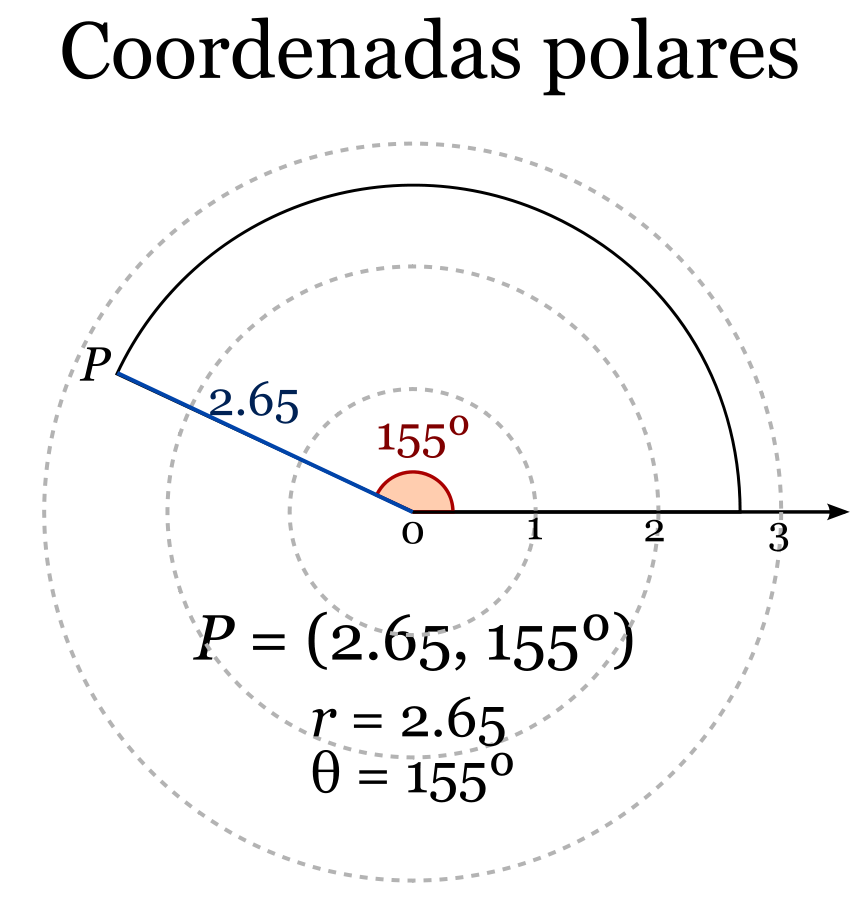
Como se aprecia en la imagen el sistema consiste en una serie de círculos concéntricos con radios de diferente longitud en el rango [0, ∞]. Cada punto en el espacio es representado por la dupla (r, θ) donde r es el radio de un círculo y θ el ángulo a partir de la recta horizontal en sentido anti-horario. Dependiendo de la unidad en que se midan los ángulos θ puede tomar los valores [ − π, π] o [0, 2π] si la unidad es el radián, o bien [0, 360∘] si la unidad se mide en grados.
Una vez asimilados estos conceptos podemos formular la solución. Para un polígono de N lados y radio r (radio del círculo circunscrito al polígono) las coordenadas de las N esquinas son $(r, 1\frac{2\pi}{N}), (r, 2\frac{2\pi}{N}), \ldots , (r, N\frac{2\pi}{N})$. Para el caso de la estrella de N picos se trabaja de manera similar: Se construye un polígono regular de N lados y para cada par de puntos se agrega un punto más a la mitad de estos dos con un radio menor a r y por último solo resta unir los puntos con líneas rectas.
Hablemos un poco a cerca de la implementación. El lenguaje que empleo aquí es Java pero esto puede fácilmente ser portado a cualquier otro lenguaje ya que la teoría es la misma. Veamos pues como esta conformada el área de dibujo en Java:
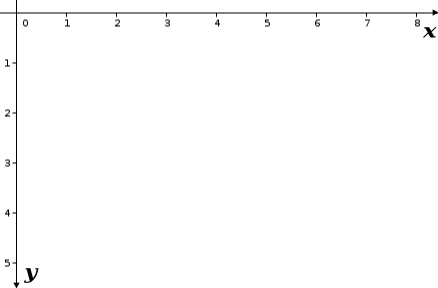
El eje x se comporta tal cual lo conocemos pero al parecer tenemos un pequeño inconveniente con el eje y que se comporta de forma inversa, cuando y aumenta el desplazamiento es hacia abajo. Es necesario aplicar una pequeña transformación al eje y para restaurar su comportamiento y de esta manera facilitarnos las cosas. La transformación que necesitamos es una reflexión:
$ y’ = maxY - y$
Donde maxY es la altura del área de dibujo. Para obtener el valor original de y a a partir de y′ empleamos la siguiente operación:
$ y = maxY - y’$
Ya casi tenemos todo listo para empezar a codificar, solo falta ver como convertir las coordenadas polares a rectangulares, pequeño detalle. De la siguiente ilustración se puede observar que tenemos los datos necesarios para obtener las componentes rectangulares de un punto.
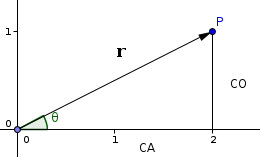
La componente horizontal es el cateto adyacente y por tanto x = rcos (θ), el cateto opuesto es la componente vertical y de ahí que y = rsin (θ). Ahora sí, al código. Veamos como quedaría el método para calcular las coordenadas de un polígono:
/**
* Compute the coordinates of a polygon.
*
* @param n number of sides
* @param center center of the polygon
* @param point point of the first corner
*/
void computePolygon(int n, Point center, Point point)
{
double r = center.distance(point),
cx = center.getX(),
cy = ly((int)center.getY()),
px = point.getX(),
py = ly((int)point.getY()),
theta = 2 * Math.PI / n,
beta = Math.atan2(py - cy, px - cx),
x, y, xPrime, yPrime;
polygon.clear();
for (int i = 0; i < n; i++) {
x = r * Math.cos(i * theta);
y = r * Math.sin(i * theta);
// Rotate the polygon such that the mouse click matches the polygon corner
xPrime = x * Math.cos(beta) - y * Math.sin(beta);
yPrime = x * Math.sin(beta) + y * Math.cos(beta);
// Translate the polygon to it's original position
xPrime += cx;
yPrime += cy;
polygon.add(new Point((int)Math.round(xPrime), (int)Math.round(yPrime)));
}
}En las líneas 25 a 27 se hace una rotación a la figura con el fin de que el primer vértice del polígono coincida con el punto donde se encuentra el apuntador del ratón. Esta transformación en realidad no forma parte del algoritmo sino más bien por estética. Los métodos int ly(int y) y int oy(int y) se encargan de obtener y′ y y respectivamente.
private int ly(int y) { return maxY - y; }
private int oy(int y) { return maxY - y; }Como pueden observer los métodos son idénticos, sin embargo el objetivo es distinto. Por claridad los emplearemos para sus respectivas funciones. El código para las estrellas es el siguiente:
/**
* Compute the coordinates of a n-pointed star.
*
* @param n number of points
* @param center star center
* @param point first point of the star
*/
void computeStar(int n, Point center, Point point)
{
double r = center.distance(point),
theta = 2 * Math.PI / n,
cx = center.getX(),
cy = ly((int)center.getY()),
px = point.getX(),
py = ly((int)point.getY()),
beta = Math.atan2(py - cy, px - cx),
x, y, xPrime, yPrime;
star.clear();
for (int i = 0; i < n; i++) {
x = r * Math.cos(i * theta);
y = r * Math.sin(i * theta);
// Rotate the polygon such that the mouse click matches the star point
xPrime = x * Math.cos(beta) - y * Math.sin(beta);
yPrime = x * Math.sin(beta) + y * Math.cos(beta);
// Translate to it's original position
xPrime += cx;
yPrime += cy;
star.add(new Point((int)Math.round(xPrime), (int)Math.round(yPrime)));
x = 0.5 * r * Math.cos(i * theta + 0.5 * theta);
y = 0.5 * r * Math.sin(i * theta + 0.5 * theta);
xPrime = x * Math.cos(beta) - y * Math.sin(beta);
yPrime = x * Math.sin(beta) + y * Math.cos(beta);
xPrime += cx;
yPrime += cy;
star.add(new Point((int)Math.round(xPrime), (int)Math.round(yPrime)));
}
}Ahora solo resta construir una interfaz para la aplicación, sin embargo eso esta fuera del alcance de este post así que no entraremos en detalles. Al final les dejo el código completo de la aplicación por si acaso. He aquí el resultado:
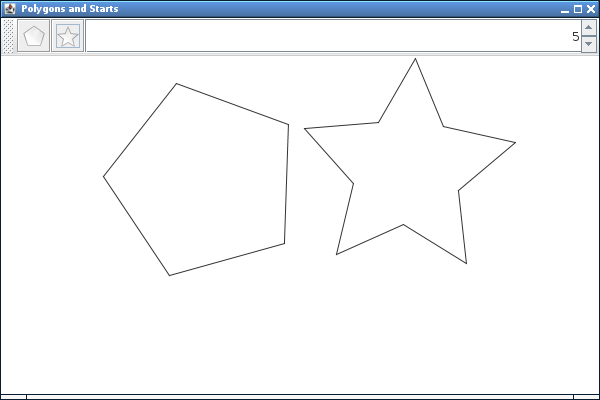
Hasta aquí con este post, espero les sea de utilidad. He de comentarles que este tema de los gráficos por computadora es uno de mis temas favoritos ya que es aquí donde encuentro una aplicación práctica e interesante a tanta teoría de mis cursos de matemáticas. Tengo planes de hacer una serie de artículos a cerca de estos temas con más detalle y aplicaciones. Hasta la próxima!
Referencias
- Computer Graphics for Java Programmers, Second Edition by Leen AmmeraalandKang Zhang
- Coordenadas polares, Wikipedia
- Coordenadas cartesianas, Wikipedia