Systems of linear equations are very important and has many applications in real life, from the most obvious to find the intersection point of many linear equations in the plane, upto the analysis of electronic circuits with Kirchhoff's laws or traffic flow in streets.
I am not an expert in this topics but currently we are studying this topic in my numerical methods course, since the course is about "numerical" methods, we don't study the Gaussian elimination method because it is more algebraic, instead we study Jacobi method. I am going to explain briefly the idea of the method and I give you a simple implementation in Java.
Jacobi method
This was the first iterative method to solve systems of linear equations and was devised by Carl Gustav Jacob Jacobi(1804-1851). Lets define the system of linear equations as:
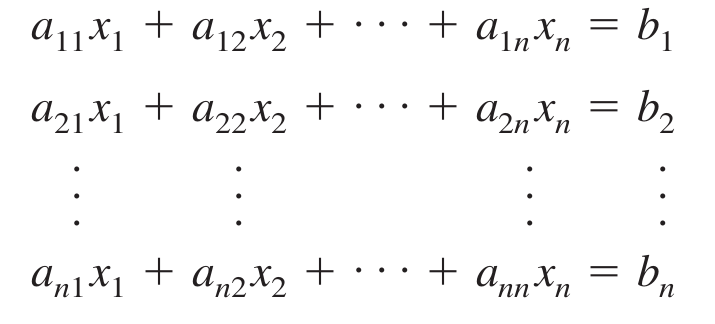
Figure 1. Equation system.
For each row i isolate the $x\_{i}$ variable.
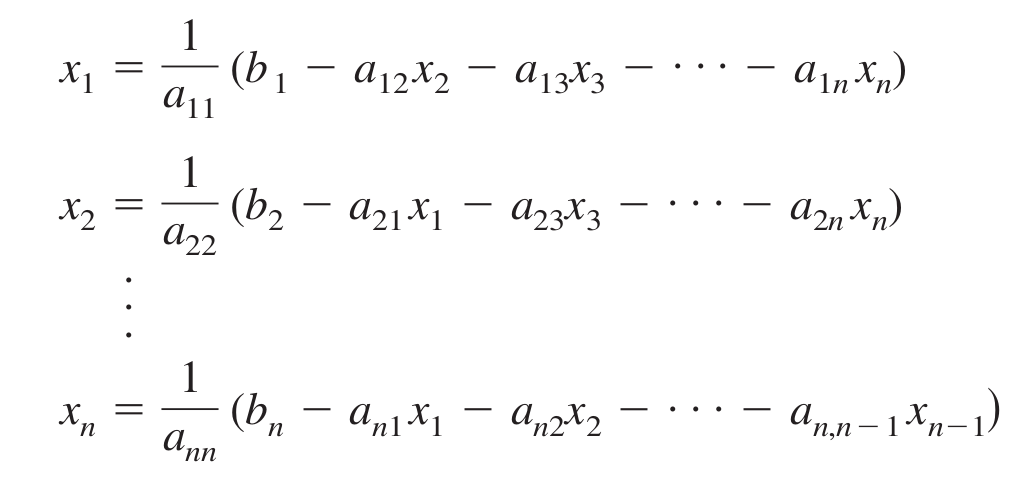
Figure 2. Isolate variables.
Make an initial approximation of the solution $(x_{1}, x_{2}, x_{3},\ldots,x_{n})$, a good choice is to use zero to all variables. Substitute these values in the rewritten equation and update the values of the approximation. Repeat the process until the answer be acceptable.
Stop condition
You can stop the iterations when $ |x\_{n+1} - x\_{n}| \leq \epsilon$ for all $x\_{i}$, $n$ is the number of iterations.
Convergence condition
Only if the coefficient matrix is diagonally dominant the method can guarantee a convergence to the solution. Sometimes the convergence can be achieved even if the conditions are not satisfied, but there is no guarantee.
Implementation in Java
/* * This class provides a simple implementation of the Jacobi method for solving
* systems of linear equations. */
/*
How to use:
The program reads an augmented matrix from standard input,
for example:
3
5 -2 3 -1
-3 9 1 2
2 -1 -7 3
The number in the first line is the number of equations
and number of variables. You can put this values in a file
and then execute the program as follows:
$ java Jacobi < equations.txt
If the matrix isn't diagonally dominant the program tries
to convert it(if possible) by rearranging the rows.
*/
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Jacobi {
public static final int MAX_ITERATIONS = 100;
private double[][] M;
public Jacobi(double [][] matrix) { M = matrix; }
public void print()
{
int n = M.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n + 1; j++)
System.out.print(M[i][j] + " ");
System.out.println();
}
}
public boolean transformToDominant(int r, boolean[] V, int[] R)
{
int n = M.length;
if (r == M.length) {
double[][] T = new double[n][n+1];
for (int i = 0; i < R.length; i++) {
for (int j = 0; j < n + 1; j++)
T[i][j] = M[R[i]][j];
}
M = T;
return true;
}
for (int i = 0; i < n; i++) {
if (V[i]) continue;
double sum = 0;
for (int j = 0; j < n; j++)
sum += Math.abs(M[i][j]);
if (2 * Math.abs(M[i][r]) > sum) { // diagonally dominant?
V[i] = true;
R[r] = i;
if (transformToDominant(r + 1, V, R))
return true;
V[i] = false;
}
}
return false;
}
/**
* Returns true if is possible to transform M(data member) to a diagonally
* dominant matrix, false otherwise.
*/
public boolean makeDominant()
{
boolean[] visited = new boolean[M.length];
int[] rows = new int[M.length];
Arrays.fill(visited, false);
return transformToDominant(0, visited, rows);
}
/**
* Applies Jacobi method to find the solution of the system
* of linear equations represented in matrix M.
* M is a matrix with the following form:
* a_11 * x_1 + a_12 * x_2 + ... + a_1n * x_n = b_1
* a_21 * x_1 + a_22 * x_2 + ... + a_2n * x_n = b_2
* . . . .
* . . . .
* . . . .
* a_n1 * x_n + a_n2 * x_2 + ... + a_nn * x_n = b_n
*/
public void solve()
{
int iterations = 0;
int n = M.length;
double epsilon = 1e-15;
double[] X = new double[n]; // Approximations
double[] P = new double[n]; // Prev
Arrays.fill(X, 0);
Arrays.fill(P, 0);
while (true) {
for (int i = 0; i < n; i++) {
double sum = M[i][n]; // b_n
for (int j = 0; j < n; j++)
if (j != i)
sum -= M[i][j] * P[j];
// Update x_i but it's no used in the next row calculation
// but up to de next iteration of the method
X[i] = 1/M[i][i] * sum;
}
System.out.print("X_" + iterations + " = {");
for (int i = 0; i < n; i++)
System.out.print(X[i] + " ");
System.out.println("}");
iterations++;
if (iterations == 1) continue;
boolean stop = true;
for (int i = 0; i < n && stop; i++)
if (Math.abs(X[i] - P[i]) > epsilon)
stop = false;
if (stop || iterations == MAX_ITERATIONS) break;
P = (double[])X.clone();
}
}
public static void main(String[] args) throws IOException
{
int n;
double[][] M;
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
PrintWriter writer = new PrintWriter(System.out, true);
n = Integer.parseInt(reader.readLine());
M = new double[n][n+1];
for (int i = 0; i < n; i++) {
StringTokenizer strtk = new StringTokenizer(reader.readLine());
while (strtk.hasMoreTokens())
for (int j = 0; j < n + 1 && strtk.hasMoreTokens(); j++)
M[i][j] = Integer.parseInt(strtk.nextToken());
}
Jacobi jacobi = new Jacobi(M);
if (!jacobi.makeDominant()) {
writer.println("The system isn't diagonally dominant: " +
"The method cannot guarantee convergence.");
}
writer.println();
jacobi.print();
jacobi.solve();
}
}
Gauss-Seidel Method
This is modification of the Jacobi method made by Carl Friedrich Gauss and Philipp L. Seidel that can converge in less iterations than Jacobi method. In the Jacobi method the values of the approximations $x_{i}$ are used up to the next iteration of the method while in the Gauss-Seidel version each approximation $x_{i}$ is used as soon as it's ready, see the code to a better understanding. Since the two methods are very similar I show only the fragment where the codes differ.Arrays.fill(X, 0);
while (true) {
for (int i = 0; i < n; i++) {
double sum = M[i][n]; // b_n
for (int j = 0; j < n; j++)
if (j != i)
sum -= M[i][j] * X[j];
// Update x_i to use in the next row calculation
X[i] = 1/M[i][i] * sum;
}
Comparison
If we solve the following system of linear equations we get to the answer at different rates.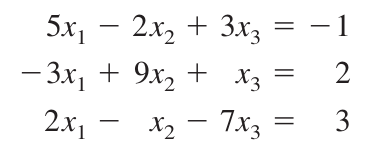
Figure 3. Example.
X_28 = {0.18611987381703476 0.3312302839116719 -0.42271293375394314 }
while Gauss-Seidel only needs 17:
X_17 = {0.18611987381703465 0.3312302839116719 -0.42271293375394325 }
Conclusion
I think these methods are easier to remember than the Gaussian elimination method and can be very useful when you have a computer and an approximated result is acceptable, for example, in a programming contest :). I hope it be useful for you, Bye!References
| 1 | Iterative methods for solving linear systems |
| 2 | Jacobi method, Wikipedia |