El día de hoy estuve resolviendo este problema y les quiero compartir mi solución y un poco del análisis para poder resolverlo.
Debido a las restricciones del problema, realizar la simulación no es factible, así que habrá que buscar otra forma. Empecemos por analizar el ejemplo de entrada:
4 5 1 6 5 9 14 15 11 26 25 29 54 55 51 106 105 109 214 215 211
Calculemos la suma de cada fila:
4 + 5 + 1 = 10 6 + 5 + 9 = 20 14 + 15 + 11 = 40 26 + 25 + 29 = 80 54 + 55 + 51 = 160 106+ 105+ 109 = 320 214+ 215+ 211 = 640
¿Notan el patrón? ¿No? Bueno, otro ejemplo:
7 4 5 3 12 15 14 16 45 42 43 41 126 129 128 130 387 384 385 383 1152 1155 1154 1156
Y las sumas son:
7 + 4 + 5 + 3 = 19 12 + 15 + 14 + 16 = 57 45 + 42 + 43 + 41 = 171 126 + 129 + 128 + 130 = 513 387 + 384 + 385 + 383 = 1539 1152 + 1155 + 1154 + 1156 = 4617
Las sumas a partir de la segunda fila corresponden la suma de la fila anterior multiplicada por $n - 1$, donde $n$ es el número de columnas (el número de vacas que tiene el granjero Juan), en nuestro segundo ejemplo $n = 4$ y por lo tanto $3 * 19 = 57$, $3 * 57 = 171$, etc.
Ahora veamos como calculamos el resultado de una de la primera columna:
$1539 - 513 + 171 - 57 + 19 - 7 = 1152$ $513 - 171 + 57 - 19 + 7 = 387$Con un poco de observación llegamos a que el resultado final de una vaca $i$ es igual a:
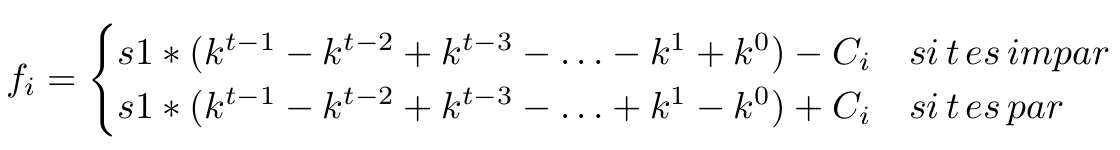
Figura 1. Formula para obtener el resultado final.
Donde $k = n - 1$, $s1$ es la suma de la primera fila y $C_{i}$ es el valor inicial de la vaca $i$.
El problema en estas expresiones es que $t$ es demasiado grande como para iterar y calcular el resultado, intente simplificar el problema pero no llegue a nada, hice una pregunta en math.stackexchange.com y me proporcionaron una formula que en efecto responde a mi pregunta, sin embargo, no pude aplicar esa formula a este problema ya que las propiedades de módulo no se aplican con las divisiones.
Después de investigar llegue a que necesitamos utilizar la siguiente matriz:
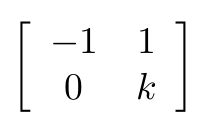
Figura 2. Matriz base.
Elevamos esta matriz a la potencia $t$ y podremos encontrar el valor que buscamos en $M_{0,1}$. Para que la exponenciación funcione en tiempo debemos utilizar el método de exponenciación binaria que tiene una complejidad $O(log_{2} n)$, siendo $n$ el valor del exponente.
Sin más aquí les dejo mi código:
#include <iostream>
#include <cassert>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 50005;
const long long mod = 98765431;
long long C[N];
class Matrix {
public:
Matrix()
{
_rows = 0;
_cols = 0;
}
Matrix(int r, int c)
{
_rows = r;
_cols = c;
}
long long * operator[](int index)
{
return _m[index];
}
Matrix operator*(Matrix &B) const
{
int i, j, k;
Matrix C(rows(), B.cols());
for (i = 0; i < rows(); i++) {
for (j = 0; j < B.cols(); j++) {
C[i][j] = 0;
for (k = 0; k < cols(); k++)
C[i][j] = (C[i][j] + _m[i][k] * B[k][j]) % mod;
}
}
return C;
}
Matrix& operator=(Matrix right)
{
_rows = right.rows();
_cols = right.cols();
for (int i = 0; i < right.rows(); i++)
for (int j = 0; j < right.cols(); j++)
_m[i][j] = right[i][j];
return *this;
}
Matrix operator^(int p) const
{
p--;
Matrix a = *this;
Matrix b = *this;
while (p > 0) {
if (p % 2 == 1)
a = a * b;
p /= 2;
b = b * b;
}
return a;
}
int cols() const { return _cols; }
int rows() const { return _rows; }
void print()
{
for (int i = 0; i < rows(); i++) {
printf("|");
for (int j = 0; j < cols(); j++)
printf("%lld ", _m[i][j]);
printf("|\n");
}
}
private:
int _rows, _cols;
long long _m[5][5];
};
int main(int argc, char **argv)
{
long long n, t, sum = 0;
int i;
scanf("%lld %lld", &n, &t);
for (i = 0; i < n; i++) {
scanf("%lld", &C[i]);
sum += C[i];
}
sum %= mod;
Matrix m(2, 2);
m[0][0] = -1;
m[0][1] = 1;
m[1][0] = 0;
m[1][1] = n - 1;
Matrix b = m^t;
long long x = (sum * b[0][1]) % mod;
for (i = 0; i < n; i++) {
if (t % 2 == 1) {
printf("%lld\n", (x - C[i] + mod) % mod);
} else {
printf("%lld\n", (x + C[i]) % mod);
}
}
return 0;
}
Hay que tener mucho cuidado con los desbordamientos en los tipos de datos y con valores negativos, en este caso en particular ayuda mucho utilizar un tipo long long, sin embargo, esto no es suficiente para todos los casos, es por ellos que hay que realizar la operación módulo en varios puntos.
Espero que les sea de utilidad. Hasta la próxima.