Z algorithm
String matching is a very common problem, given a text T and a pattern P find the occurrences of P in T. This problem doesn’t need too much introduction.
The most easy (and naive) algorithm to solve this problem is to slide off P through T and see if there is a match. Something like this:
for (int i = 0; i + P.length <= T.length; i++) {
int j = 0;
while (P[j] == T[i+j])
j++;
if (j == P.length)
// We found a match!
}However, much more efficient solutions exists to this problem, the Z algorithm is one of them.
The Zi(T) function
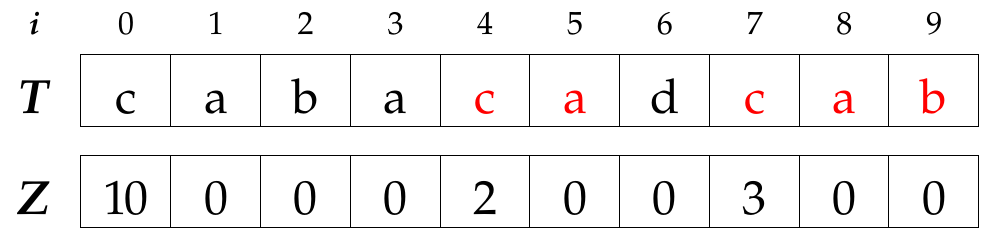
The Zi(T) is equal to the length of the longest substring starting at position i > 0 that matches a prefix of T.
For example, let be T = “cabacadcab”, Z3 = 0, Z4 = 2 and Z7 = 3. Obviously Z0 is always equal to the length of the string. See figure .
Z Boxes
If $Z_{i} > 0$ a Z-box is a substring that starts at position $i$ and ends at position $i + Z_{i} - 1$, i.e. the substring that matches the prefix of $T$.Assume that we have already computed the values of Z upto some k − 1 and now we need to compute Zk. There are four possible cases. In the following pictures l and r denote de start and the end of the last Z-box.
Case 1: $ k $ is out of the last Z-box
Position k is not contained in the last Z-box. We need to compare character by character to find Zk.
Case 2: $ k $ is within the last Z-box
We’ll denote this last Z-box as α and as β the box starting at position k and ending at r. Since every Z-box matches a prefix, the following figure depicts our situation.
As you can see, k′ corresponds to position k in the prefix and we already computed Zk′ and so we can leverage this fact. There are three more cases.
Case 2a: $ Z_{k’} < |\beta| $
In this case Zk = Zk′.
Case 2b: $ Z_{k’} > |\beta| $
Let be x the first character that is not contained in the last Z-box and y the first character that is not contained in the prefix, we know one thing, x ≠ y and therefore Zk cannot be greater than Zk′. Result Zk = |β|.
Case 2c: $ Z_{k’} = || $
Here we know two things, x ≠ y and y ≠ w. How about x and w? We don’t know, they may be equal or not. In this case it’s necessary to verify.
Okay, here is an implementation to complement the explanation:
Z[0] = n;
int l = 0, r = 0;
for (int k = 1; k < n; k++) {
if (r < k) {
l = r = k;
while (S[r] == S[r-l])
r++;
Z[k] = r - l;
} else {
int b = r - k;
int j = k - l; // j is k'
if (Z[j] < b) {
Z[k] = Z[j];
} else if (Z[j] > b) {
Z[k] = b;
} else {
l = k;
r = k + b;
while (S[r] == S[r-l])
r++;
Z[k] = r - l;
}
}
}Since l and r never decrease the complexity of this algorithm is O(n).
String matching using the Z function
Now that we know how to compute the Z function let’s see how to use it to find the occurrences of a pattern P in a text T. The idea is easy:
- Concatenate P with T and compute the Z function in the resulting string (S = P + T )
- There is an occurrence of P that start at position i > = |P| if Zi(S) > = |P|.
Practice problems
Here are some problems to put into practice this algorithm:
- Codeforces Round #246 Div 2 Problem D: Prefixes and Suffixes | My solution
- Light OJ: 1255 - Substring Frequency | My solution